Integración por partes
Integración por partes
Aprendizaje personal
En nuestra clase vimos un tema llamado integración por partes que es una herramienta esencial en el campo del cálculo integral. Se basa en una versión modificada de la regla del producto en la derivación y es especialmente útil cuando necesitas encontrar la integral de un producto de dos funciones.
Conocimiento complementario
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
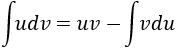
Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).
Aunque se trata de un método simple, hay que aplicarlo correctamente.
Método:
- El integrando debe ser un producto de dos factores (si no lo es, podemos transformarlo para que lo sea).
- Uno de los factores será y el otro será .
- Se calcula derivando y se calcula integrando .
- Se aplica la fórmula.
-
- Logarítmicas (por ejemplo, (\ln x))
- Inversas trigonométricas (por ejemplo, (\arctan x))
- Algebraicas (por ejemplo, (x^2))
- Trigonométricas (por ejemplo, (\sin x))
- Exponenciales (por ejemplo, (e^x))
integral 1
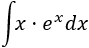 SOLUCIÓN
SOLUCIÓNTenemos el producto .
Observad que la exponencial no cambia al derivar ni al integrar, así que no importa si le asignamos ó .
No ocurre lo mismo con :
- Al derivar se reduce su exponente en 1 y pasa a ser una constante.
- Al integrar aumenta su exponente en 1.
Por tanto, la elección más apropiada es y .
Derivamos para calcular :
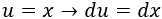
Integramos para calcular :
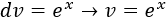
Aplicamos la fórmula de integración por partes:
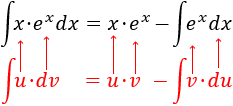
Finalmente, resolvemos la nueva integral (la de la exponencial) y añadimos la constante de integración :
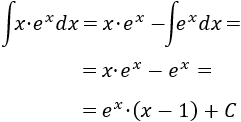
Nota: como ya hemos dicho, es importante escoger para reducir el grado del monomio al derivar. Si por el contrario hubiésemos escogido , entonces , aumentando el grado (de 1 a 2) y complicando más la integral, pues el factor de la exponencial se mantiene igual y nos aparece la integral
Comentario:
- En la integral anterior hemos considerado , pero algunos autores habrían escrito simplemente (es decir, sin ). No es algo que afecte a la resolución de la integral.
- También, podemos encontrar puntos multiplicativos en la fórmula de integración por partes, como en , que facilitan diferenciar los elementos de la fórmula.
Integral 2 
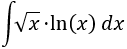
La única dificultad de esta integral es integrar la raíz cuadrada.
Como ya hemos venido diciendo, escogemos y, por tanto, .
Derivamos para calcular :
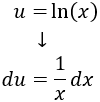
Integramos para calcular (escribiendo la raíz cuadrada como una potencia):
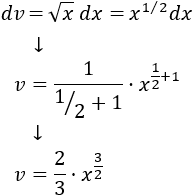
Aplicamos la fórmula de integración por partes:
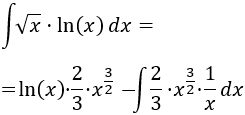
Operamos un poco y resolvemos:
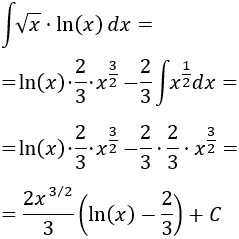
Imágenes
Videos por enlace



Comentarios
Publicar un comentario